Computes the hinge loss for a one-of-many classification task. More...
#include <hinge_loss_layer.hpp>
Public Member Functions | |
| HingeLossLayer (const LayerParameter ¶m) | |
| virtual const char * | type () const |
| Returns the layer type. | |
 Public Member Functions inherited from caffe::LossLayer< Dtype > Public Member Functions inherited from caffe::LossLayer< Dtype > | |
| LossLayer (const LayerParameter ¶m) | |
| virtual void | LayerSetUp (const vector< Blob< Dtype > *> &bottom, const vector< Blob< Dtype > *> &top) |
| Does layer-specific setup: your layer should implement this function as well as Reshape. More... | |
| virtual void | Reshape (const vector< Blob< Dtype > *> &bottom, const vector< Blob< Dtype > *> &top) |
| Adjust the shapes of top blobs and internal buffers to accommodate the shapes of the bottom blobs. More... | |
| virtual int | ExactNumBottomBlobs () const |
| Returns the exact number of bottom blobs required by the layer, or -1 if no exact number is required. More... | |
| virtual bool | AutoTopBlobs () const |
| For convenience and backwards compatibility, instruct the Net to automatically allocate a single top Blob for LossLayers, into which they output their singleton loss, (even if the user didn't specify one in the prototxt, etc.). | |
| virtual int | ExactNumTopBlobs () const |
| Returns the exact number of top blobs required by the layer, or -1 if no exact number is required. More... | |
| virtual bool | AllowForceBackward (const int bottom_index) const |
 Public Member Functions inherited from caffe::Layer< Dtype > Public Member Functions inherited from caffe::Layer< Dtype > | |
| Layer (const LayerParameter ¶m) | |
| void | SetUp (const vector< Blob< Dtype > *> &bottom, const vector< Blob< Dtype > *> &top) |
| Implements common layer setup functionality. More... | |
| Dtype | Forward (const vector< Blob< Dtype > *> &bottom, const vector< Blob< Dtype > *> &top) |
| Given the bottom blobs, compute the top blobs and the loss. More... | |
| void | Backward (const vector< Blob< Dtype > *> &top, const vector< bool > &propagate_down, const vector< Blob< Dtype > *> &bottom) |
| Given the top blob error gradients, compute the bottom blob error gradients. More... | |
| vector< shared_ptr< Blob< Dtype > > > & | blobs () |
| Returns the vector of learnable parameter blobs. | |
| const LayerParameter & | layer_param () const |
| Returns the layer parameter. | |
| virtual void | ToProto (LayerParameter *param, bool write_diff=false) |
| Writes the layer parameter to a protocol buffer. | |
| Dtype | loss (const int top_index) const |
| Returns the scalar loss associated with a top blob at a given index. | |
| void | set_loss (const int top_index, const Dtype value) |
| Sets the loss associated with a top blob at a given index. | |
| virtual int | MinBottomBlobs () const |
| Returns the minimum number of bottom blobs required by the layer, or -1 if no minimum number is required. More... | |
| virtual int | MaxBottomBlobs () const |
| Returns the maximum number of bottom blobs required by the layer, or -1 if no maximum number is required. More... | |
| virtual int | MinTopBlobs () const |
| Returns the minimum number of top blobs required by the layer, or -1 if no minimum number is required. More... | |
| virtual int | MaxTopBlobs () const |
| Returns the maximum number of top blobs required by the layer, or -1 if no maximum number is required. More... | |
| virtual bool | EqualNumBottomTopBlobs () const |
| Returns true if the layer requires an equal number of bottom and top blobs. More... | |
| bool | param_propagate_down (const int param_id) |
| Specifies whether the layer should compute gradients w.r.t. a parameter at a particular index given by param_id. More... | |
| void | set_param_propagate_down (const int param_id, const bool value) |
| Sets whether the layer should compute gradients w.r.t. a parameter at a particular index given by param_id. | |
Protected Member Functions | |
| virtual void | Forward_cpu (const vector< Blob< Dtype > *> &bottom, const vector< Blob< Dtype > *> &top) |
| Computes the hinge loss for a one-of-many classification task. More... | |
| virtual void | Backward_cpu (const vector< Blob< Dtype > *> &top, const vector< bool > &propagate_down, const vector< Blob< Dtype > *> &bottom) |
| Computes the hinge loss error gradient w.r.t. the predictions. More... | |
 Protected Member Functions inherited from caffe::Layer< Dtype > Protected Member Functions inherited from caffe::Layer< Dtype > | |
| virtual void | Forward_gpu (const vector< Blob< Dtype > *> &bottom, const vector< Blob< Dtype > *> &top) |
| Using the GPU device, compute the layer output. Fall back to Forward_cpu() if unavailable. | |
| virtual void | Backward_gpu (const vector< Blob< Dtype > *> &top, const vector< bool > &propagate_down, const vector< Blob< Dtype > *> &bottom) |
| Using the GPU device, compute the gradients for any parameters and for the bottom blobs if propagate_down is true. Fall back to Backward_cpu() if unavailable. | |
| virtual void | CheckBlobCounts (const vector< Blob< Dtype > *> &bottom, const vector< Blob< Dtype > *> &top) |
| void | SetLossWeights (const vector< Blob< Dtype > *> &top) |
Additional Inherited Members | |
 Protected Attributes inherited from caffe::Layer< Dtype > Protected Attributes inherited from caffe::Layer< Dtype > | |
| LayerParameter | layer_param_ |
| Phase | phase_ |
| vector< shared_ptr< Blob< Dtype > > > | blobs_ |
| vector< bool > | param_propagate_down_ |
| vector< Dtype > | loss_ |
Detailed Description
template<typename Dtype>
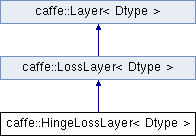
class caffe::HingeLossLayer< Dtype >
Computes the hinge loss for a one-of-many classification task.
- Parameters
-
bottom input Blob vector (length 2) 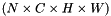 the predictions
the predictions 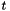 , a Blob with values in
, a Blob with values in ![$ [-\infty, +\infty] $](form_17.png) indicating the predicted score for each of the
indicating the predicted score for each of the 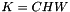 classes. In an SVM,
classes. In an SVM, 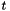 is the result of taking the inner product
is the result of taking the inner product 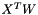 of the D-dimensional features
of the D-dimensional features 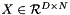 and the learned hyperplane parameters
and the learned hyperplane parameters 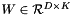 , so a Net with just an InnerProductLayer (with num_output = D) providing predictions to a HingeLossLayer and no other learnable parameters or losses is equivalent to an SVM.
, so a Net with just an InnerProductLayer (with num_output = D) providing predictions to a HingeLossLayer and no other learnable parameters or losses is equivalent to an SVM.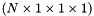 the labels
the labels 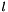 , an integer-valued Blob with values
, an integer-valued Blob with values ![$ l_n \in [0, 1, 2, ..., K - 1] $](form_24.png) indicating the correct class label among the
indicating the correct class label among the 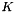 classes
classes
top output Blob vector (length 1) 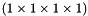 the computed hinge loss:
the computed hinge loss: ![$ E = \frac{1}{N} \sum\limits_{n=1}^N \sum\limits_{k=1}^K [\max(0, 1 - \delta\{l_n = k\} t_{nk})] ^ p $](form_93.png) , for the
, for the 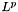 norm (defaults to
norm (defaults to 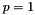 , the L1 norm; L2 norm, as in L2-SVM, is also available), and
, the L1 norm; L2 norm, as in L2-SVM, is also available), and 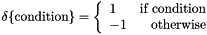
In an SVM, 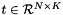 is the result of taking the inner product
is the result of taking the inner product 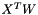 of the features
of the features 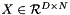 and the learned hyperplane parameters
and the learned hyperplane parameters 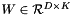 . So, a Net with just an InnerProductLayer (with num_output =
. So, a Net with just an InnerProductLayer (with num_output = 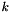 ) providing predictions to a HingeLossLayer is equivalent to an SVM (assuming it has no other learned outside the InnerProductLayer and no other losses outside the HingeLossLayer).
) providing predictions to a HingeLossLayer is equivalent to an SVM (assuming it has no other learned outside the InnerProductLayer and no other losses outside the HingeLossLayer).
Member Function Documentation
◆ Backward_cpu()
|
protectedvirtual |
Computes the hinge loss error gradient w.r.t. the predictions.
Gradients cannot be computed with respect to the label inputs (bottom[1]), so this method ignores bottom[1] and requires !propagate_down[1], crashing if propagate_down[1] is set.
- Parameters
-
top output Blob vector (length 1), providing the error gradient with respect to the outputs propagate_down see Layer::Backward. propagate_down[1] must be false as we can't compute gradients with respect to the labels. bottom input Blob vector (length 2) 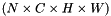 the predictions
the predictions 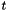 ; Backward computes diff
; Backward computes diff 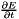
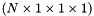 the labels – ignored as we can't compute their error gradients
the labels – ignored as we can't compute their error gradients
Implements caffe::Layer< Dtype >.
◆ Forward_cpu()
|
protectedvirtual |
Computes the hinge loss for a one-of-many classification task.
- Parameters
-
bottom input Blob vector (length 2) 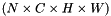 the predictions
the predictions 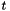 , a Blob with values in
, a Blob with values in ![$ [-\infty, +\infty] $](form_17.png) indicating the predicted score for each of the
indicating the predicted score for each of the 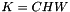 classes. In an SVM,
classes. In an SVM, 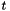 is the result of taking the inner product
is the result of taking the inner product 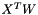 of the D-dimensional features
of the D-dimensional features 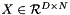 and the learned hyperplane parameters
and the learned hyperplane parameters 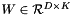 , so a Net with just an InnerProductLayer (with num_output = D) providing predictions to a HingeLossLayer and no other learnable parameters or losses is equivalent to an SVM.
, so a Net with just an InnerProductLayer (with num_output = D) providing predictions to a HingeLossLayer and no other learnable parameters or losses is equivalent to an SVM.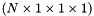 the labels
the labels 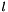 , an integer-valued Blob with values
, an integer-valued Blob with values ![$ l_n \in [0, 1, 2, ..., K - 1] $](form_24.png) indicating the correct class label among the
indicating the correct class label among the 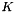 classes
classes
top output Blob vector (length 1) 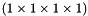 the computed hinge loss:
the computed hinge loss: ![$ E = \frac{1}{N} \sum\limits_{n=1}^N \sum\limits_{k=1}^K [\max(0, 1 - \delta\{l_n = k\} t_{nk})] ^ p $](form_93.png) , for the
, for the 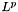 norm (defaults to
norm (defaults to 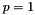 , the L1 norm; L2 norm, as in L2-SVM, is also available), and
, the L1 norm; L2 norm, as in L2-SVM, is also available), and 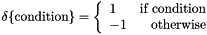
In an SVM, 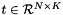 is the result of taking the inner product
is the result of taking the inner product 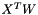 of the features
of the features 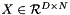 and the learned hyperplane parameters
and the learned hyperplane parameters 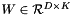 . So, a Net with just an InnerProductLayer (with num_output =
. So, a Net with just an InnerProductLayer (with num_output = 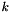 ) providing predictions to a HingeLossLayer is equivalent to an SVM (assuming it has no other learned outside the InnerProductLayer and no other losses outside the HingeLossLayer).
) providing predictions to a HingeLossLayer is equivalent to an SVM (assuming it has no other learned outside the InnerProductLayer and no other losses outside the HingeLossLayer).
Implements caffe::Layer< Dtype >.
The documentation for this class was generated from the following files:
- include/caffe/layers/hinge_loss_layer.hpp
- src/caffe/layers/hinge_loss_layer.cpp
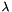 , as
, as 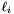 in the overall
in the overall 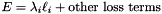 ; hence
; hence 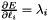 . (*Assuming that this top
. (*Assuming that this top  1.8.13
1.8.13