Here are the classes, structs, unions and interfaces with brief descriptions:
[detail level 1234]
| ▼Ncaffe | A layer factory that allows one to register layers. During runtime, registered layers can be called by passing a LayerParameter protobuffer to the CreateLayer function: |
| ►Ndb | |
| CAbsValLayer | Computes 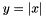 |
| CAccuracyLayer | Computes the classification accuracy for a one-of-many classification task |
| CAdaDeltaSolver | |
| CAdaGradSolver | |
| CAdamSolver | AdamSolver, an algorithm for first-order gradient-based optimization of stochastic objective functions, based on adaptive estimates of lower-order moments. Described in [1] |
| CArgMaxLayer | Compute the index of the 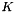 max values for each datum across all dimensions max values for each datum across all dimensions  |
| CBaseConvolutionLayer | Abstract base class that factors out the BLAS code common to ConvolutionLayer and DeconvolutionLayer |
| CBaseDataLayer | Provides base for data layers that feed blobs to the Net |
| CBasePrefetchingDataLayer | |
| CBatch | |
| CBatchNormLayer | Normalizes the input to have 0-mean and/or unit (1) variance across the batch |
| CBatchReindexLayer | Index into the input blob along its first axis |
| CBiasLayer | Computes a sum of two input Blobs, with the shape of the latter Blob "broadcast" to match the shape of the former. Equivalent to tiling the latter Blob, then computing the elementwise sum |
| CBilinearFiller | Fills a Blob with coefficients for bilinear interpolation |
| CBlob | A wrapper around SyncedMemory holders serving as the basic computational unit through which Layers, Nets, and Solvers interact |
| ►CBlockingQueue | |
| CBNLLLayer | Computes 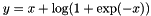 if if 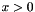 ; ; 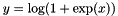 otherwise otherwise |
| ►CCaffe | |
| CConcatLayer | Takes at least two Blobs and concatenates them along either the num or channel dimension, outputting the result |
| CConstantFiller | Fills a Blob with constant values 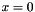 |
| CContrastiveLossLayer | Computes the contrastive loss 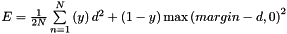 where where 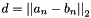 . This can be used to train siamese networks . This can be used to train siamese networks |
| CConvolutionLayer | Convolves the input image with a bank of learned filters, and (optionally) adds biases |
| CCPUTimer | |
| CCropLayer | Takes a Blob and crop it, to the shape specified by the second input Blob, across all dimensions after the specified axis |
| CDataLayer | |
| CDataTransformer | Applies common transformations to the input data, such as scaling, mirroring, substracting the image mean.. |
| CDeconvolutionLayer | Convolve the input with a bank of learned filters, and (optionally) add biases, treating filters and convolution parameters in the opposite sense as ConvolutionLayer |
| CDropoutLayer | During training only, sets a random portion of 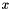 to 0, adjusting the rest of the vector magnitude accordingly to 0, adjusting the rest of the vector magnitude accordingly |
| CDummyDataLayer | Provides data to the Net generated by a Filler |
| CEltwiseLayer | Compute elementwise operations, such as product and sum, along multiple input Blobs |
| CELULayer | Exponential Linear Unit non-linearity 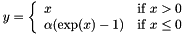 |
| CEmbedLayer | A layer for learning "embeddings" of one-hot vector input. Equivalent to an InnerProductLayer with one-hot vectors as input, but for efficiency the input is the "hot" index of each column itself |
| CEuclideanLossLayer | Computes the Euclidean (L2) loss 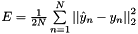 for real-valued regression tasks for real-valued regression tasks |
| CExpLayer | Computes 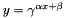 , as specified by the scale , as specified by the scale 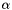 , shift , shift 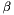 , and base , and base 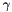 |
| CFiller | Fills a Blob with constant or randomly-generated data |
| CFilterLayer | Takes two+ Blobs, interprets last Blob as a selector and filter remaining Blobs accordingly with selector data (0 means that the corresponding item has to be filtered, non-zero means that corresponding item needs to stay) |
| CFlattenLayer | Reshapes the input Blob into flat vectors |
| CGaussianFiller | Fills a Blob with Gaussian-distributed values 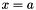 |
| CHDF5DataLayer | Provides data to the Net from HDF5 files |
| CHDF5OutputLayer | Write blobs to disk as HDF5 files |
| CHingeLossLayer | Computes the hinge loss for a one-of-many classification task |
| CIm2colLayer | A helper for image operations that rearranges image regions into column vectors. Used by ConvolutionLayer to perform convolution by matrix multiplication |
| CImageDataLayer | Provides data to the Net from image files |
| CInfogainLossLayer | A generalization of MultinomialLogisticLossLayer that takes an "information gain" (infogain) matrix specifying the "value" of all label pairs |
| CInnerProductLayer | Also known as a "fully-connected" layer, computes an inner product with a set of learned weights, and (optionally) adds biases |
| CInputLayer | Provides data to the Net by assigning tops directly |
| CInternalThread | |
| CLayer | An interface for the units of computation which can be composed into a Net |
| CLayerRegisterer | |
| CLayerRegistry | |
| CLogLayer | Computes 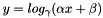 , as specified by the scale , as specified by the scale 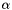 , shift , shift 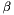 , and base , and base 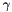 |
| CLossLayer | An interface for Layers that take two Blobs as input – usually (1) predictions and (2) ground-truth labels – and output a singleton Blob representing the loss |
| CLRNLayer | Normalize the input in a local region across or within feature maps |
| CLSTMLayer | Processes sequential inputs using a "Long Short-Term Memory" (LSTM) [1] style recurrent neural network (RNN). Implemented by unrolling the LSTM computation through time |
| CLSTMUnitLayer | A helper for LSTMLayer: computes a single timestep of the non-linearity of the LSTM, producing the updated cell and hidden states |
| CMemoryDataLayer | Provides data to the Net from memory |
| CMSRAFiller | Fills a Blob with values 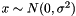 where where 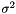 is set inversely proportional to number of incoming nodes, outgoing nodes, or their average is set inversely proportional to number of incoming nodes, outgoing nodes, or their average |
| CMultinomialLogisticLossLayer | Computes the multinomial logistic loss for a one-of-many classification task, directly taking a predicted probability distribution as input |
| CMVNLayer | Normalizes the input to have 0-mean and/or unit (1) variance |
| CNesterovSolver | |
| ►CNet | Connects Layers together into a directed acyclic graph (DAG) specified by a NetParameter |
| CNeuronLayer | An interface for layers that take one blob as input ( 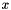 ) and produce one equally-sized blob as output ( ) and produce one equally-sized blob as output ( 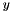 ), where each element of the output depends only on the corresponding input element ), where each element of the output depends only on the corresponding input element |
| CParameterLayer | |
| CPoolingLayer | Pools the input image by taking the max, average, etc. within regions |
| CPositiveUnitballFiller | Fills a Blob with values ![$ x \in [0, 1] $](form_3.png) such that such that 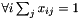 |
| CPowerLayer | Computes 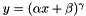 , as specified by the scale , as specified by the scale 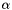 , shift , shift 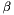 , and power , and power 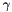 |
| CPReLULayer | Parameterized Rectified Linear Unit non-linearity 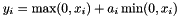 . The differences from ReLULayer are 1) negative slopes are learnable though backprop and 2) negative slopes can vary across channels. The number of axes of input blob should be greater than or equal to 2. The 1st axis (0-based) is seen as channels . The differences from ReLULayer are 1) negative slopes are learnable though backprop and 2) negative slopes can vary across channels. The number of axes of input blob should be greater than or equal to 2. The 1st axis (0-based) is seen as channels |
| CPythonLayer | |
| CRecurrentLayer | An abstract class for implementing recurrent behavior inside of an unrolled network. This Layer type cannot be instantiated – instead, you should use one of its implementations which defines the recurrent architecture, such as RNNLayer or LSTMLayer |
| CReductionLayer | Compute "reductions" – operations that return a scalar output Blob for an input Blob of arbitrary size, such as the sum, absolute sum, and sum of squares |
| CReLULayer | Rectified Linear Unit non-linearity 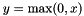 . The simple max is fast to compute, and the function does not saturate . The simple max is fast to compute, and the function does not saturate |
| CReshapeLayer | |
| CRMSPropSolver | |
| CRNNLayer | Processes time-varying inputs using a simple recurrent neural network (RNN). Implemented as a network unrolling the RNN computation in time |
| CScaleLayer | Computes the elementwise product of two input Blobs, with the shape of the latter Blob "broadcast" to match the shape of the former. Equivalent to tiling the latter Blob, then computing the elementwise product. Note: for efficiency and convenience, this layer can additionally perform a "broadcast" sum too when bias_term: true is set |
| CSGDSolver | Optimizes the parameters of a Net using stochastic gradient descent (SGD) with momentum |
| CSigmoidCrossEntropyLossLayer | Computes the cross-entropy (logistic) loss ![$ E = \frac{-1}{n} \sum\limits_{n=1}^N \left[ p_n \log \hat{p}_n + (1 - p_n) \log(1 - \hat{p}_n) \right] $](form_163.png) , often used for predicting targets interpreted as probabilities , often used for predicting targets interpreted as probabilities |
| CSigmoidLayer | Sigmoid function non-linearity 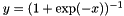 , a classic choice in neural networks , a classic choice in neural networks |
| CSignalHandler | |
| CSilenceLayer | Ignores bottom blobs while producing no top blobs. (This is useful to suppress outputs during testing.) |
| CSliceLayer | Takes a Blob and slices it along either the num or channel dimension, outputting multiple sliced Blob results |
| CSoftmaxLayer | Computes the softmax function |
| CSoftmaxWithLossLayer | Computes the multinomial logistic loss for a one-of-many classification task, passing real-valued predictions through a softmax to get a probability distribution over classes |
| ►CSolver | An interface for classes that perform optimization on Nets |
| CSolverRegisterer | |
| CSolverRegistry | |
| CSplitLayer | Creates a "split" path in the network by copying the bottom Blob into multiple top Blobs to be used by multiple consuming layers |
| CSPPLayer | Does spatial pyramid pooling on the input image by taking the max, average, etc. within regions so that the result vector of different sized images are of the same size |
| CSyncedMemory | Manages memory allocation and synchronization between the host (CPU) and device (GPU) |
| CTanHLayer | TanH hyperbolic tangent non-linearity 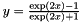 , popular in auto-encoders , popular in auto-encoders |
| CThresholdLayer | Tests whether the input exceeds a threshold: outputs 1 for inputs above threshold; 0 otherwise |
| CTileLayer | Copy a Blob along specified dimensions |
| CTimer | |
| CUniformFiller | Fills a Blob with uniformly distributed values 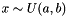 |
| CWindowDataLayer | Provides data to the Net from windows of images files, specified by a window data file. This layer is DEPRECATED and only kept for archival purposes for use by the original R-CNN |
| CXavierFiller | Fills a Blob with values 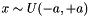 where where 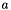 is set inversely proportional to number of incoming nodes, outgoing nodes, or their average is set inversely proportional to number of incoming nodes, outgoing nodes, or their average |
 1.8.13
1.8.13